2024国家公务员行测备考：三集合容斥问题怎么解

　　2024国家公务员行测备考：三集合容斥问题怎么解由国家公务员考试网整理发布。更多关于行测备考,2024国考,2024国家公务员,以及公务员考试备考信息。请关注国家公务员考试网/内蒙古人事考试网！

2024国考公告预约

职位查询

领航计划

历年分数线

图书网课

笔试课程

　　2024国家公务员行测备考：三集合容斥问题怎么解

　　>>>2024国家公务员考试备考技巧

　　在公务员考试中，行测和申论同样重要，而在行测中，数量关系可能是很多同学放弃的一部分。一方面大家对于数量关系或多或少存在畏难情绪，另一方面考试时间有限，很多同学做到数量的时候已经快要交卷了，于是大部分人放弃了这一部分。然而近几年在国考和部分省考中，数量关系的题目有简单易做的趋势，建议各位考生抓住数量关系中的基础知识点，才能做到解题游刃有余。今天，小编就给大家来讲讲三集合容斥问题该怎么求解。

　　首先什么是容斥问题呢?一个大的集合按照不同的标准或条件，划分成几个小的集合，即为容斥问题。举个小例子，一个班级共50人，数学考试及格的有39人，语文考试及格的有45人，两门考试全通过的有33人。这个小例子中我们发现，按照数学考试和语文考试是否及格给班级50人划分成了好几个小的部分，那么这就是容斥问题。这个小例子中有2个划分的条件，我们叫做二集合容斥问题，若有3个划分的条件，就是三集合容斥问题。在三集合容斥问题中，有两个计算公式，那么这两个公式什么时候用哪个，该怎么区分呢?下面我们一起来看一下：

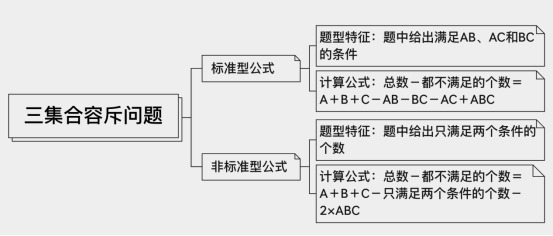
　　1、三集合容斥标准型公式：总数-都不满足的个数=A+B+C-AB-BC-AC+ABC。

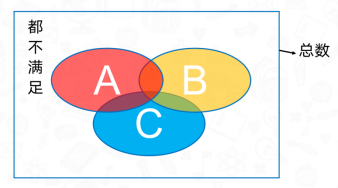
　　当我们发现题目中给了满足AB的条件、满足AC的条件、满足BC的条件，可以代入三集合容斥标准型公式中列式计算，那么下面让我们看一道例题。

　　【例1】某学校共有50名学生，现学院举办各类竞赛。其中，参加数学竞赛的有26人，参加英语竞赛的有27人，参加计算机竞赛的有28人。同时参加数学竞赛和英语竞赛的学生有18人，同时参加英语竞赛和计算机竞赛的有16人，同时参加数学竞赛和计算机竞赛的有12人，三种竞赛均参加的人数为10人，问该学院没有参加任何竞赛的同学有几人?

　　A. 5人 B. 6人

　　C. 7人 D. 8人

　　题目中按照是否参加各类竞赛，给50名同学划分成了几个小的部分，属于容斥问题，且有3个划分的条件，即为三集合容斥问题。发现题中给了同时参加数学竞赛和英语竞赛、同时参加英语竞赛和计算机竞赛和同时参加数学竞赛和计算机竞赛的人数，直接代入三集合容斥标准型公式中即可。根据题意可列式：26+27+28-18-16-12+10=50-都不参加的人数。解得都不参加的人数为5人。因此，本题选择A选项。

　　2、三集合容斥非标准型公式：总数-都不满足的个数=A+B+C-只满足两个条件的个数-2×ABC。

　　当我们发现题目中并没有给满足AB、AC和BC的条件，而给的是只满足两个条件的个数，这时，我们需要代入三集合容斥非标准型公式计算。让我们看一道例题来巩固一下：

　　【例2】某单位组织职工棋牌赛，希望全体职工根据自己的兴趣爱好报名参赛，报名表提交工会后，根据统计发现，报名参加围棋比赛的有63人，报名参加象棋比赛的有89人，报名参加桥牌比赛的有47人，三种比赛都报名参加的24人，报名参加两种比赛的46人，任何比赛都不报名的15人。问：该单位共有多少名职工?

　　A. 55 B. 144

　　C. 120 D. 116

　　题目中按照是否参加各类比赛，给职工划分成了几个小的部分，属于容斥问题，且有3个划分的条件，即为三集合容斥问题。发现题中给的是报名参加两种比赛的人数，需要代入三集合容斥非标准型公式中计算。根据题意可列式：63+89+47-46-2×24=总人数-15。解得总人数为120人。因此，本题选择C选项。

　　以上就是三集合容斥问题的两个计算公式，大家都掌握了吗。

　　 　　　

　　以上是关于2024国家公务员行测备考：三集合容斥问题怎么解的全部内容，更多关于行测备考,2024国考,2024国家公务员的相关信息敬请加入国家公务员考试群 ，及关注国家公务员考试网。

（编辑：haibing）